I had another stimulating discussion with Noah Smith last week. This time the topic was the ‘loanable funds’ theory of the rate of interest. The discussion was triggered by my suggestion that the ‘safe asset shortage’ and associated ‘reach for yield’ are in part caused by rising wealth concentration. The logic is straightforward: since the rich spend less of their income than the poor, wealth concentration tends to increase the rate of saving out of income. This means an increase in desired savings chasing the available stock of financial assets, pushing up the price and lowering the yield.
Noah viewed this as a plausible hypothesis but suggested it relies on the loanable funds model. My view was the opposite – I think this mechanism is incompatible with the loanable funds theory. Such disagreements are often enlightening – either one of us misunderstood the mechanisms under discussion, or we were using different definitions. My instinct was that it was the latter: we meant something different by ‘loanable funds theory’ (LFT hereafter).
To try and clear this up, Noah suggested Mankiw’s textbook as a starting point – and found a set of slides which set out the LFT clearly. The model described was exactly the one I had in mind – but despite agreeing that Mankiw’s exposition of the LFT was accurate it was clear we still didn’t agree about the original point of discussion.
The reason seems to be that Noah understands the LFT to describe any market for loans: there are some people willing to lend and some who wish to borrow. As the rate of interest rises, the volume of available lending increases but the volume of desired borrowing falls. In equilibrium, the rate of interest will settle at r* – the market-clearing rate.
What’s wrong with this? – It certainly sounds like a market for ‘loanable funds’. The problem is that LFT is not a theory of loan market clearing per se. It’s a theory of macroeconomic equilibrium. It’s not a model of any old loan market: it’s a model of a one very specific market – the market which intermediates total (net) saving with total capital investment in a closed economic system.
OK, but saving equals investment by definition in macroeconomic terms: the famous S = I identity. How can there be a market which operates to ensure equality between two identically equal magnitudes?
The issue – as Keynes explained in the General Theory– is that in a modern capitalist economy, the person who saves and the person who undertakes fixed capital investment are not usually the same. Some mechanism needs to be in place to ensure that a decision to ‘not consume’ somewhere in the system – to save – is always matched by a decision to invest – to build a new machine, road or building – somewhere else in the economy.
To see the issue more clearly consider the ‘corn economy’ used in many standard macro models: one good – corn – is produced. This good can either be consumed or invested (by planting in the ground or storing corn for later consumption). The decision to plant or store corn is simultaneously both a decision to ‘not consume’ and to ‘invest’ (the rate of return on investment will depend on the mix of stored to planted corn). In this simple economy S = I because it can’t be any other way. A market for loanable funds is not required.
But this isn’t how modern capitalism works. Decisions to ‘not consume’ and decisions to invest are distributed throughout the economic system. How can we be sure that these decisions will lead to identical intended saving and investment – what ensures that S and I are equal? The loanable funds theory provides one possible answer to this question.
The theory states that decisions to save (i.e. to not consume) are decisive – investment adjusts automatically to accommodate any change in consumption behaviour. To see how this works, we need to recall how the model is derived. The diagram below shows the basic system (I’ve borrowed the figure from Nick Rowe).
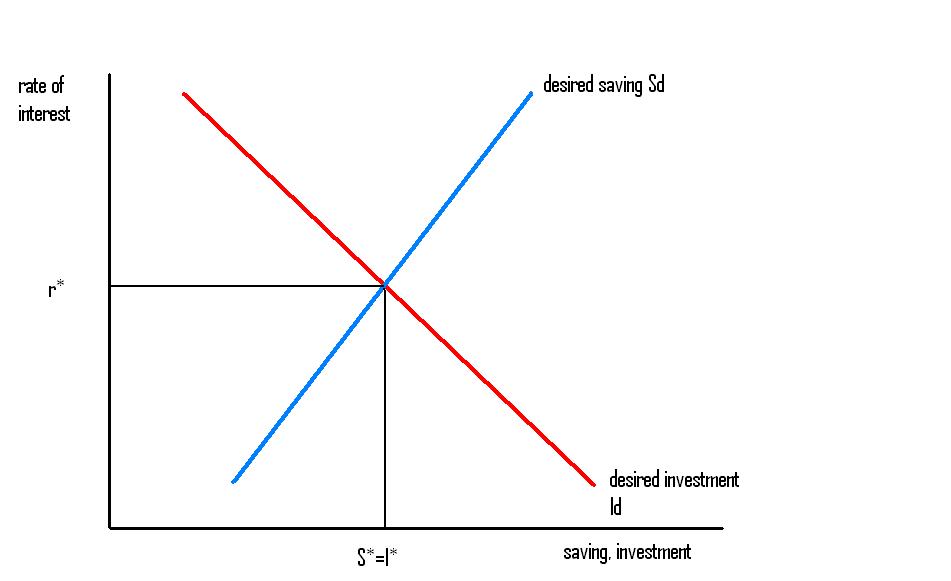
The upward sloping ‘desired saving’ curve is derived on the assumption that people are ‘impatient’ – they prefer current consumption to future consumption. In order to induce people to save, a return needs to be paid on their savings. As the return paid on savings increases, consumers are collectively willing to forgo a greater volume of current consumption in return for a future payoff.
The downward sloping investment curve is derived on standard neoclassical marginalist principles. ‘Factors of production’ (i.e. labour and capital) receive ‘what they are worth’ in competitive markets. The real wage is equal to the marginal productivity of labour and the return on ‘capital’ is likewise equal to the marginal productivity of capital. As the ‘quantity’ of capital increases, the marginal product – and thus the rate of return – falls.
So the S and I curves depict how much saving and investment would take place at each possible rate of interest. As long as the S and I curves are well-defined and ‘monotonic’ (a strong assumption), there is only one rate of interest at which the amount people wish to lend is equal to the amount (other) people would like to borrow. This is r*, the point of intersection between the curves. This rate of interest is often referred to as the Wicksellian ‘natural rate’.
Now, consider what happens if the collective impatience of society decreases. At any rate of interest, consumption as a share of income will be lower and desired saving correspondingly higher – the S curve moves to the right. As the S curve shifts to the right – assuming no change in the technology determining the slope and position of the I curve – a greater share of national income is ‘not consumed’. But by pushing down the rate of interest in the loanable funds market, reduced consumption – somewhat miraculously – leads to an automatic increase in investment. An outward shift in the S curve is accompanied by a shift along the I curve.
Consider what this means for macroeconomic aggregates. Assuming a closed system, income is, by definition, equal to consumption plus investment: Y = C + I. The LFT says is that in freely adjusting markets, reductions in C due to shifts in preferences are automatically offset by increases in I. Y will remain at the ‘full employment’ rate of output at all times.
The LFT therefore underpins ‘Say’s Law’ – summarised by Keynes as ‘supply creates its own demand’. It was thus a key target for Keynes’ attack on the ‘Law’ in his General Theory. Keynes argued against the notion that saving decisions are strongly influenced by the rate of interest. Instead, he argued consumption is mostly determined by income. If individuals consume a fixed proportion of their income, the S curve in the diagram is no longer well defined – at any given level of output, S is vertical, but the position of the curve shifts with output. This is quite different to the LFT which regards the position of the two curves as determined by the ‘deep’ structural parameters of the system – technology and preferences.
How then is the rate of interest determined in Keynes’ theory? – the answer is ‘liquidity preference’. Rather than desired saving determining the rate of interest, what matters is the composition of financial assets people use to hold their savings. Keynes simplifies the story by assuming only two assets: ‘money’ which pays no interest and ‘bonds’ which do pay interest. It is the interaction of supply and demand in the bond market – not the ‘loanable funds’ market – which determines the rate of interest.
There are two key points here: the first is that saving is a residual – it is determined by output and investment. As such, there is no mechanism to ensure that desired saving and desired investment will be equalised. This means that output, not the rate of interest, will adjust to ensure that saving is equal to investment. There is no mechanism which ensures that output is maintained at full employment levels. The second is that interest rates can move without any change in either desired saving or desired investment. If there is an increase in ‘liquidity preference’ – a desire to hold lower yielding but safer assets, this will cause an increase in the rate of interest on riskier assets.
How can the original question be framed using these two models? – What is the implication of increasing wealth concentration on yields and macro variables?
I think Noah is right that one can think of the mechanism in a loanable funds world. If redistribution towards the rich increases the average propensity to save, this will shift the S curve to the right – as in the example above – reducing the ‘natural’ rate of interest. This is the standard ‘secular stagnation’ story – a ‘global savings glut’ has pushed the natural rate below zero. However, in a loanable funds world this should – all else being equal – lead to an increase in investment. This doesn’t seem to fit the stylised facts: capital investment has been falling as a share of GDP in most advanced nations. (Critics will point out that I’m skirting the issue of the zero lower bound – I’ll have to save that for another time).
My non-LFT interpretation is the following. Firstly, I’d go further than Keynes and argue that the rate of interest is not only relatively unimportant for determining S – it also has little effect on I. There is evidence to suggest that firms’ investment decisions are fairly interest-inelastic. This means that both curves in the diagram above have a steep slope – and they shift as output changes. There is no ‘natural rate’ of interest which brings the macroeconomic system into equilibrium.
In terms of the S = I identity, this means that investment decisions are more important for the determination of macro variables than saving decisions. If total desired saving as a share of income increases – due to wealth concentration, for example – this will have little effect on investment. The volume of realised saving, however, is determined by (and identically equal to) the volume of capital investment. An increase in desired saving manifests itself not as a rise in investment – but as a fall in consumption and output.
In such a scenario – in which a higher share of nominal income is saved – the result will be weak demand for goods but strong demand for financial assets – leading to deflation in the goods market and inflation in the market for financial assets. Strong demand for financial assets will reduce rates of return – but only on financial assets: if investment is inelastic to interest rate there is no reason to believe there will be any shift in investment or in the return on fixed capital investment.
In order explain the relative rates of return on equity and bonds, a re-working of Keynes’ liquidity preference theory is required. Instead of a choice between ‘money’ and ‘bonds’, the choice faced by investors can be characterised as a choice between risky equity and less-risky bonds. Liquidity preference will then make itself felt as an increase in the price of bonds relative to equity – and a corresponding movement in the yields on each asset. On the other hand, an increase in total nominal saving will increase the price of all financial assets and thus reduce yields across the board. Given that it is likely that portfolio managers will have minimum target rates of return, this is will induce a shift into higher-risk assets.
“Firstly, I’d go further than Keynes and argue that the rate of interest is not only relatively unimportant for determining S – it also has little effect on I. There is evidence to suggest that firms’ investment decisions are fairly interest-inelastic.”
This is a good first step in understanding why nearly everything that Keynes said in The General Theory is wrong. It was stated by Lawrence Klein a few decades ago (see A History of Macroeconomics from Keynes to Lucas and Beyond by Michel De Vroey)
The next step is to understand that what is important is not the complement of consumption (which is investment) but the obverse of consumption (which is production). You have more or less stated that too.
The fall in investment is a consequence of the fall in consumption, not the cause of it.
The final step is to understand that Keynes’s theory of liquidity preference comes from a complete misunderstanding of the nature of money. If you wish to relate money to aggregate consumption then you must treat money as a means of exchange, not as an asset (which is what both Keynes and Friedman did). It is saving which is related to assets.
The slowdown in the US economy is a consequence of the rise in the saving rate (note SAVING RATE, not merely SAVING) from 3% before the crash to 6% for an extended period since then.
All this does not mean that Keynes was wrong and the DSGE school right. Keynes was wrong about a whole lot of things but he was right about the fundamentals: Involuntary Unemployment and Aggregate Demand.
I have touched upon these issues in my Amazon ebook: Macroeconomics Redefined.
LikeLike
I think one element missing is how the central banks react to all this. Even if we don’t go full ‘horizontalist’, there is a substantial degree to which they can counter the upward pressures from on asset prices wealth concentration, at least for some assets (e.g. short-term bonds). Or conversely, they may fuel the process by lowering interest rates, in order to get asset price inflation.
I would also add that, beside wealth concentration, institutionalisation of savings through pension funds and such, plays a similar important role.
LikeLike
Bruno, thanks. Yes, I skirted the whole issue of banking and financial institutions – I wanted to focus on the LFT for this one. I will come back to it and write something on the banking and financial side of things.
LikeLike
Nice post.
Except that LFT is deeply incoherent in a way that simply cannot admit any kind of logical reverse engineering or sensible interpretation. It is conceptual nonsense.
First, the constant equivalence of I and S is a national income accounting fact.
Second, that equivalence absolutely does not reference “funds” in any sense. This is income accounting, not flow of funds accounting. There is nothing in the concept of S and I that assumes anything whatsoever about the texture of the financial intermediation that may lie between them.
Third, the I curve has potential meaning in a way in which the S curve does not. It would be possible as a concept to consider realized I as a function of r, however strangely that function may behave But the notion of a planned S that somehow intersects with a realized I is simply incoherent. Once I is realized, S is realized. S cannot create I. And this equivalence is continous and constant – at every theoretical second of accounting. The S curve is meaningless and redundant – it can’t possibly explain economic adjustment because it implicitly portrays impossible accounting adjustment – because such adjustment simply doesn’t exist. I determines S at all times.
This is fundamental to Keynes’ GT – he anticipated coherent national income accounting and revised his I and S relationship from what was in the Treatise. His liquidity preference theory is essentially a recognition that flow of funds accounting is different than national income accounting. FF accounting is essential in the explanation of interest rates. While the correct accounting doesn’t explain the economics, it is foundational in the explanation. The S curve floats nonsensically in the ether.
LikeLiked by 1 person
“In such a scenario – in which a higher share of nominal income is saved – the result will be weak demand for goods but strong demand for financial assets – leading to deflation in the goods market and inflation in the market for financial assets.”
I would go further than this. A higher share of income being saved does not in itself imply strong demand for financial assets, because (as you have explained) the actual quantity of a savings is no higher. Any substitution effect towards financial assets is exactly offset by an income effect. It is only when the policy response to weak demand for goods is looser monetary policy that there might be any increase in the price of financial assets.
LikeLiked by 1 person
My own comment on this: http://monetaryreflections.blogspot.co.uk/2016/10/wealth-concentration-and-loanable-funds.html
LikeLiked by 1 person
A lot of bullshit. DFIs create new money when they lend/invest. They do not loan out existing deposits saved or otherwise. Therefore R* is an impossible construct.
LikeLiked by 1 person